在three.js中, BufferGeometry 是用来代表所有几何体的一种方式。 BufferGeometry 本质上是一系列 BufferAttributes 的 名称 。每一个 BufferAttribute 代表一种类型数据的数组:位置,法线,颜色,uv,等等…… 这些合起来, BufferAttributes 代表每个顶点所有数据的 并行数组 。
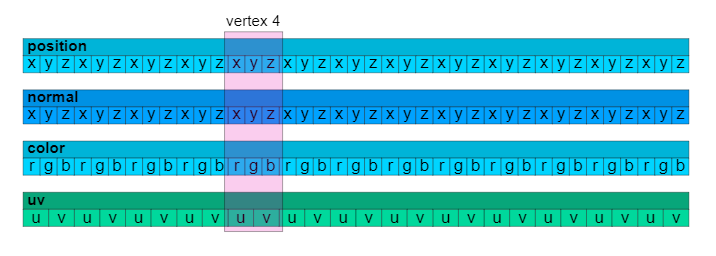
上面提到,我们有四个属性:position, normal, color, uv 。 它们指的是 并行数组 ,代表每个属性的第N个数据集属于同一个顶点。index=4的顶点被高亮表示贯穿所有属性的平行数据定义一个顶点。
这就告诉我们,这是一个方块的数据图,高亮的地方代表一个角。
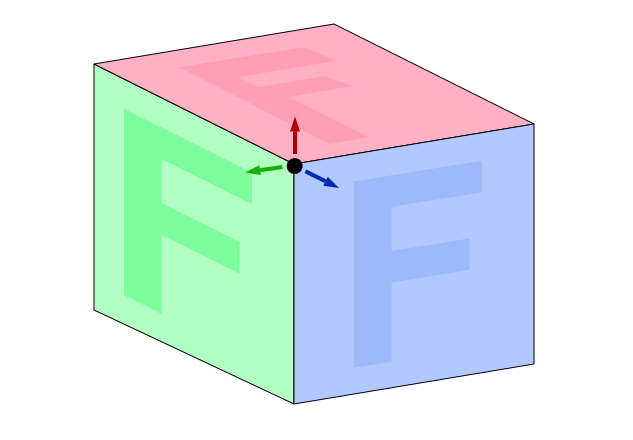
考虑下方块的单个角,不同的面都需要一个不同的法线。法线是面朝向的信息。在图中,在方块的角周围用箭头表示的法线,代表共用顶点位置的面需要指向不同方向的法线。
同理,一个角在不同的面需要不同的UVs。UVs是用来指定纹理区域中,画在相应顶点位置三角形的纹理坐标。你可以看到,绿色的面需要顶点的UV对应于F纹理的右上角,蓝色的面需要的UV对应于F纹理的左上角,红色的面需要的UV对应于F纹理的左下角。
一个简单的 顶点 是所有组成部分的集合。如果顶点需要其中任一部分变得不同,那么它必须是一个不同的顶点。
举一个简单的例子,让我们创建一个使用 BufferGeometry 的方块。方块很有趣,因为它看起来在角的地方共用顶点但实际上不是。在我们的例子中,我们将列出所有顶点数据,然后转化成并行数组,最后用它们创建 BufferAttributes 并添加到 BufferGeometry 。
我们从方块所需的所有数据开始。再次记住如果顶点有任何独一无二的部分,它必须是不同的顶点。像这里创建一个方块需要36个顶点,每个面2个三角形,每个三角形3个顶点,6个面=36个顶点。
const vertices = [
// front
{ pos: [-1, -1, 1], norm: [ 0, 0, 1], uv: [0, 0], },
{ pos: [ 1, -1, 1], norm: [ 0, 0, 1], uv: [1, 0], },
{ pos: [-1, 1, 1], norm: [ 0, 0, 1], uv: [0, 1], },
{ pos: [-1, 1, 1], norm: [ 0, 0, 1], uv: [0, 1], },
{ pos: [ 1, -1, 1], norm: [ 0, 0, 1], uv: [1, 0], },
{ pos: [ 1, 1, 1], norm: [ 0, 0, 1], uv: [1, 1], },
// right
{ pos: [ 1, -1, 1], norm: [ 1, 0, 0], uv: [0, 0], },
{ pos: [ 1, -1, -1], norm: [ 1, 0, 0], uv: [1, 0], },
{ pos: [ 1, 1, 1], norm: [ 1, 0, 0], uv: [0, 1], },
{ pos: [ 1, 1, 1], norm: [ 1, 0, 0], uv: [0, 1], },
{ pos: [ 1, -1, -1], norm: [ 1, 0, 0], uv: [1, 0], },
{ pos: [ 1, 1, -1], norm: [ 1, 0, 0], uv: [1, 1], },
// back
{ pos: [ 1, -1, -1], norm: [ 0, 0, -1], uv: [0, 0], },
{ pos: [-1, -1, -1], norm: [ 0, 0, -1], uv: [1, 0], },
{ pos: [ 1, 1, -1], norm: [ 0, 0, -1], uv: [0, 1], },
{ pos: [ 1, 1, -1], norm: [ 0, 0, -1], uv: [0, 1], },
{ pos: [-1, -1, -1], norm: [ 0, 0, -1], uv: [1, 0], },
{ pos: [-1, 1, -1], norm: [ 0, 0, -1], uv: [1, 1], },
// left
{ pos: [-1, -1, -1], norm: [-1, 0, 0], uv: [0, 0], },
{ pos: [-1, -1, 1], norm: [-1, 0, 0], uv: [1, 0], },
{ pos: [-1, 1, -1], norm: [-1, 0, 0], uv: [0, 1], },
{ pos: [-1, 1, -1], norm: [-1, 0, 0], uv: [0, 1], },
{ pos: [-1, -1, 1], norm: [-1, 0, 0], uv: [1, 0], },
{ pos: [-1, 1, 1], norm: [-1, 0, 0], uv: [1, 1], },
// top
{ pos: [ 1, 1, -1], norm: [ 0, 1, 0], uv: [0, 0], },
{ pos: [-1, 1, -1], norm: [ 0, 1, 0], uv: [1, 0], },
{ pos: [ 1, 1, 1], norm: [ 0, 1, 0], uv: [0, 1], },
{ pos: [ 1, 1, 1], norm: [ 0, 1, 0], uv: [0, 1], },
{ pos: [-1, 1, -1], norm: [ 0, 1, 0], uv: [1, 0], },
{ pos: [-1, 1, 1], norm: [ 0, 1, 0], uv: [1, 1], },
// bottom
{ pos: [ 1, -1, 1], norm: [ 0, -1, 0], uv: [0, 0], },
{ pos: [-1, -1, 1], norm: [ 0, -1, 0], uv: [1, 0], },
{ pos: [ 1, -1, -1], norm: [ 0, -1, 0], uv: [0, 1], },
{ pos: [ 1, -1, -1], norm: [ 0, -1, 0], uv: [0, 1], },
{ pos: [-1, -1, 1], norm: [ 0, -1, 0], uv: [1, 0], },
{ pos: [-1, -1, -1], norm: [ 0, -1, 0], uv: [1, 1], },
];
然后我们能将它们全部转换成3个并行数组
const positions = [];
const normals = [];
const uvs = [];
for (const vertex of vertices) {
positions.push(...vertex.pos);
normals.push(...vertex.norm);
uvs.push(...vertex.uv);
}
最终我们能创建一个 BufferGeometry ,然后为每个数组创建一个 BufferAttribute 并添加到 BufferGeometry 。
const geometry = new THREE.BufferGeometry();
const positionNumComponents = 3;
const normalNumComponents = 3;
const uvNumComponents = 2;
geometry.setAttribute(
'position',
new THREE.BufferAttribute(new Float32Array(positions), positionNumComponents));
geometry.setAttribute(
'normal',
new THREE.BufferAttribute(new Float32Array(normals), normalNumComponents));
geometry.setAttribute(
'uv',
new THREE.BufferAttribute(new Float32Array(uvs), uvNumComponents));
注意名字很重要。你必须将属性的名字命名成three.js所期望的(除非你正在创建自定义着色器),在这里是 position、 normal 和 uv 。如果你想要设置顶点颜色则命名属性为 color 。
在上面我们创建了3个JavaScript原生数组, positions, normals 和 uvs 。 然后我们将他们转换为 Float32Array 的类型数组TypedArrays。 BufferAttribute 是类型数组而不是原生数组。同时 BufferAttribute 需要你设定每个顶点有多少组成成分。对于位置和法线,每个顶点我们需要3个组成成分,x、y和z。对于UVs我们需要2个,u和v。

那会是大量的数据。我们可以做点改善,可以用索引来代表顶点。看回我们的方块数据,每个面由2个三角形组成,每个三角形3个顶点,总共6个,但是其中2个是完全一样的;同样的位置,同样的法线,和同样的uv。因此,我们可以移除匹配的顶点,然后用索引代表他们。首先我们移除匹配的顶点。
const vertices = [
// front
{ pos: [-1, -1, 1], norm: [ 0, 0, 1], uv: [0, 0], }, // 0
{ pos: [ 1, -1, 1], norm: [ 0, 0, 1], uv: [1, 0], }, // 1
{ pos: [-1, 1, 1], norm: [ 0, 0, 1], uv: [0, 1], }, // 2
{ pos: [ 1, 1, 1], norm: [ 0, 0, 1], uv: [1, 1], }, // 3
// right
{ pos: [ 1, -1, 1], norm: [ 1, 0, 0], uv: [0, 0], }, // 4
{ pos: [ 1, -1, -1], norm: [ 1, 0, 0], uv: [1, 0], }, // 5
{ pos: [ 1, 1, 1], norm: [ 1, 0, 0], uv: [0, 1], }, // 6
{ pos: [ 1, 1, -1], norm: [ 1, 0, 0], uv: [1, 1], }, // 7
// back
{ pos: [ 1, -1, -1], norm: [ 0, 0, -1], uv: [0, 0], }, // 8
{ pos: [-1, -1, -1], norm: [ 0, 0, -1], uv: [1, 0], }, // 9
{ pos: [ 1, 1, -1], norm: [ 0, 0, -1], uv: [0, 1], }, // 10
{ pos: [-1, 1, -1], norm: [ 0, 0, -1], uv: [1, 1], }, // 11
// left
{ pos: [-1, -1, -1], norm: [-1, 0, 0], uv: [0, 0], }, // 12
{ pos: [-1, -1, 1], norm: [-1, 0, 0], uv: [1, 0], }, // 13
{ pos: [-1, 1, -1], norm: [-1, 0, 0], uv: [0, 1], }, // 14
{ pos: [-1, 1, 1], norm: [-1, 0, 0], uv: [1, 1], }, // 15
// top
{ pos: [ 1, 1, -1], norm: [ 0, 1, 0], uv: [0, 0], }, // 16
{ pos: [-1, 1, -1], norm: [ 0, 1, 0], uv: [1, 0], }, // 17
{ pos: [ 1, 1, 1], norm: [ 0, 1, 0], uv: [0, 1], }, // 18
{ pos: [-1, 1, 1], norm: [ 0, 1, 0], uv: [1, 1], }, // 19
// bottom
{ pos: [ 1, -1, 1], norm: [ 0, -1, 0], uv: [0, 0], }, // 20
{ pos: [-1, -1, 1], norm: [ 0, -1, 0], uv: [1, 0], }, // 21
{ pos: [ 1, -1, -1], norm: [ 0, -1, 0], uv: [0, 1], }, // 22
{ pos: [-1, -1, -1], norm: [ 0, -1, 0], uv: [1, 1], }, // 23
];
现在我们有24个唯一的顶点。然后我们为36个要画的顶点设定36个索引,通过调用 BufferGeometry.setIndex 并传入索引数组来创建12个三角形。
geometry.setAttribute(
'position',
new THREE.BufferAttribute(positions, positionNumComponents));
geometry.setAttribute(
'normal',
new THREE.BufferAttribute(normals, normalNumComponents));
geometry.setAttribute(
'uv',
new THREE.BufferAttribute(uvs, uvNumComponents));
geometry.setIndex([
0, 1, 2, 2, 1, 3, // front
4, 5, 6, 6, 5, 7, // right
8, 9, 10, 10, 9, 11, // back
12, 13, 14, 14, 13, 15, // left
16, 17, 18, 18, 17, 19, // top
20, 21, 22, 22, 21, 23, // bottom
]);
如果你没有提供法线数据的话, BufferGeometry 有个方法computeVertexNormals可以用来计算法线。不幸的是,因为如果顶点的其他数据不同的话,位置数据不能被共享,调用 computeVertexNormals 会让你的几何体像球面或者圆筒一样连接自身。

对于上面的圆筒,法线是通过 computeVertexNormals 方法创建的。 如果你仔细观察会发现在圆筒上有条缝。这是因为在圆筒的开始和结束的地方没有办法共享顶点数据,需要不同的UVs,所以该方法不知道它们是同样的顶点以平滑过度。只要知道一点,解决方法是应用自己的法线数据。
我们同样可以在一开始使用类型数组TypedArrays取代JavaScript的原生数组。 缺点是你必须在一开始定义数组的大小。当然那不是很难,但是使用原生数组我们只需要用 push 将数据加入数组并最后通过 length 查看数组大小。使用类型数组我们没有这样的方法,所以需要记录添加的数据。
在这个例子,提前计算数组长度很简单,因为我们一开始使用一大块静态数据。
const numVertices = vertices.length;
const positionNumComponents = 3;
const normalNumComponents = 3;
const uvNumComponents = 2;
const positions = new Float32Array(numVertices * positionNumComponents);
const normals = new Float32Array(numVertices * normalNumComponents);
const uvs = new Float32Array(numVertices * uvNumComponents);
let posNdx = 0;
let nrmNdx = 0;
let uvNdx = 0;
for (const vertex of vertices) {
positions.set(vertex.pos, posNdx);
normals.set(vertex.norm, nrmNdx);
uvs.set(vertex.uv, uvNdx);
posNdx += positionNumComponents;
nrmNdx += normalNumComponents;
uvNdx += uvNumComponents;
}
geometry.setAttribute(
'position',
new THREE.BufferAttribute(positions, positionNumComponents));
geometry.setAttribute(
'normal',
new THREE.BufferAttribute(normals, normalNumComponents));
geometry.setAttribute(
'uv',
new THREE.BufferAttribute(uvs, uvNumComponents));
geometry.setIndex([
0, 1, 2, 2, 1, 3, // front
4, 5, 6, 6, 5, 7, // right
8, 9, 10, 10, 9, 11, // back
12, 13, 14, 14, 13, 15, // left
16, 17, 18, 18, 17, 19, // top
20, 21, 22, 22, 21, 23, // bottom
]);
一个使用类型数组的好理由,是如果你想动态更新顶点数据的任何一部分。
因为想不起动态更新顶点数据的好例子,所以我决定创建一个球面并从中央开始进进出出地移动每个四边形。但愿它是个有用的例子。
这里是用来产生球面的位置和索引数据的代码。代码共享了四边形内的顶点数据,但是四边形之间的没有共享,因为我们需要分别地移动每个四边形。
因为我懒,所以我通过3个 Object3D 对象的层级关系,计算球面的点。关于如何计算在这篇文章有解释the article on optimizing lots of objects。
function makeSpherePositions(segmentsAround, segmentsDown) {
const numVertices = segmentsAround * segmentsDown * 6;
const numComponents = 3;
const positions = new Float32Array(numVertices * numComponents);
const indices = [];
const longHelper = new THREE.Object3D();
const latHelper = new THREE.Object3D();
const pointHelper = new THREE.Object3D();
longHelper.add(latHelper);
latHelper.add(pointHelper);
pointHelper.position.z = 1;
const temp = new THREE.Vector3();
function getPoint(lat, long) {
latHelper.rotation.x = lat;
longHelper.rotation.y = long;
longHelper.updateMatrixWorld(true);
return pointHelper.getWorldPosition(temp).toArray();
}
let posNdx = 0;
let ndx = 0;
for (let down = 0; down < segmentsDown; ++down) {
const v0 = down / segmentsDown;
const v1 = (down + 1) / segmentsDown;
const lat0 = (v0 - 0.5) * Math.PI;
const lat1 = (v1 - 0.5) * Math.PI;
for (let across = 0; across < segmentsAround; ++across) {
const u0 = across / segmentsAround;
const u1 = (across + 1) / segmentsAround;
const long0 = u0 * Math.PI * 2;
const long1 = u1 * Math.PI * 2;
positions.set(getPoint(lat0, long0), posNdx); posNdx += numComponents;
positions.set(getPoint(lat1, long0), posNdx); posNdx += numComponents;
positions.set(getPoint(lat0, long1), posNdx); posNdx += numComponents;
positions.set(getPoint(lat1, long1), posNdx); posNdx += numComponents;
indices.push(
ndx, ndx + 1, ndx + 2,
ndx + 2, ndx + 1, ndx + 3,
);
ndx += 4;
}
}
return {positions, indices};
}
然后我们像这样调用。
const segmentsAround = 24;
const segmentsDown = 16;
const {positions, indices} = makeSpherePositions(segmentsAround, segmentsDown);
因为返回的位置数据是单位球面位置,所以它们跟我们需要的法线数据完全一样,我们只需要复制它们。
const normals = positions.slice();
然后我们像之前一样设置属性
const geometry = new THREE.BufferGeometry();
const positionNumComponents = 3;
const normalNumComponents = 3;
const positionAttribute = new THREE.BufferAttribute(positions, positionNumComponents);
positionAttribute.setUsage(THREE.DynamicDrawUsage);
geometry.setAttribute(
'position',
positionAttribute);
geometry.setAttribute(
'normal',
new THREE.BufferAttribute(normals, normalNumComponents));
geometry.setIndex(indices);
我已经高亮一些区别。我们保存了位置属性的引用。 同时我们标记它为动态。这是提示THREE.js我们将会经常改变属性的内容。
在我们的渲染循环中,每一帧我们基于它们的法线更新位置
const temp = new THREE.Vector3();
...
for (let i = 0; i < positions.length; i += 3) {
const quad = (i / 12 | 0);
const ringId = quad / segmentsAround | 0;
const ringQuadId = quad % segmentsAround;
const ringU = ringQuadId / segmentsAround;
const angle = ringU * Math.PI * 2;
temp.fromArray(normals, i);
temp.multiplyScalar(THREE.MathUtils.lerp(1, 1.4, Math.sin(time + ringId + angle) * .5 + .5));
temp.toArray(positions, i);
}
positionAttribute.needsUpdate = true;
我们设置 positionAttribute.needsUpdate 告诉THREE.js更新我们的改变。

我希望这些例子能对如何使用 BufferGeometry 直接创建你自己的几何体和如何动态更新 BufferAttribute 的内容发挥作用。
